如图,抛物线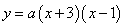 与
与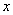 轴交于A,B两点(点A在点B右侧),过点A的直线交抛物线于另一点C
轴交于A,B两点(点A在点B右侧),过点A的直线交抛物线于另一点C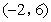 ,P是线段AC上一动点,过点P作y轴的平行线,交抛物线于点M,交x轴于点N.当
,P是线段AC上一动点,过点P作y轴的平行线,交抛物线于点M,交x轴于点N.当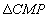 与
与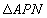 相似时,点M的坐标为( )
相似时,点M的坐标为( )
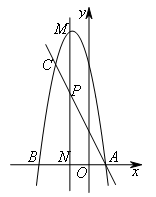
- A.
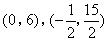
- B.
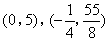
- C.
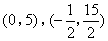
- D.
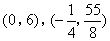
答案
正确答案:D
1.解题要点
①首先研究基本图形,求出抛物线解析式,点A,B,C的坐标,以及直线AC的解析式.
②分析![]() 和
和![]() ,只有A,C是定点,其余都是动点,
,只有A,C是定点,其余都是动点,![]() 中,∠PNA=90°,∠NPA=∠MPC属于不变特征,
中,∠PNA=90°,∠NPA=∠MPC属于不变特征,
若两个三角形相似,只需要保证![]() 中有一个角是直角,
中有一个角是直角,
即分类是:∠MCP=90°,∠CMP=90°.
③分别画出符合题意的图形求解.
2.解题过程
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
①当∠CMP=∠ANP=90°时,
∵∠APN=∠CPM,
∴△ANP∽△CMP.
此时∠MCP=∠NAP,
∴MC∥AN,如图所示,
容易求得点![]() .
.
②当∠PCM=∠PNA=90°时,△MCP∽△ANP,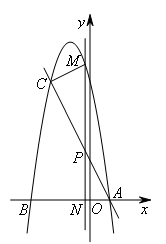
∵CM⊥AC,![]() ,
,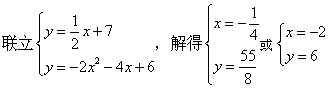 ,
,
∴![]() .
.
综上,符合题意的点M的坐标为![]() .
.
略








