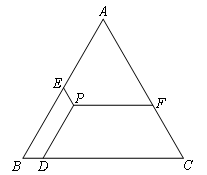
如图，P是等边三角形ABC内一点，PD∥AB交BC于点D，PE∥AC交AB于点E，PF∥BC交AC于点F，若△ABC的周长为12，则PD+PE+PF的值为(    )

思考方向：把3条内部的线段往外转移，向已知等边三角形靠拢，联系多组平行，可考虑利用平行四边形转移．
如图，延长EP交BC于点M，延长FP交AB于点N．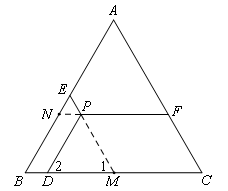

在等边三角形ABC中，=3BC，∠B=∠C=60°．
∵PF//BC，PE∥AC，
∴四边形PMCF是平行四边形，∠1=∠C=60°，
∴PF=MC．
∵PD//AB，
∴∠2=∠B=60°，
∴∠1=∠2=60°，
∴△PDM是等边三角形，
∴PD=MD．
同上，可证四边形PNBD是平行四边形，△PEN是等边三角形，
∴PN=BD，PE=PN，
∴PE=BD，
∴PD+PE+PF=MD+BD+MC=BC．
∵△ABC的周长为12，即3BC=12，
∴BC=4，
∴PD+PE+PF=4．
故选C．

略