如图,在平行四边形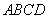 中,AB=2AD,∠A=60°,E,F分别为AB,CD的中点.
中,AB=2AD,∠A=60°,E,F分别为AB,CD的中点.
若EF=1cm,则对角线BD的长为( )
- A.1cm
- B.2cm
- C.
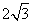 cm
cm - D.
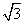 cm
cm
答案
正确答案:D
知识点:等边三角形的性质 平行四边形的性质 平行四边形的判定
思考方向:由AB=2AD,∠A=60°,可考虑构造等边三角形.
如图,连接DE.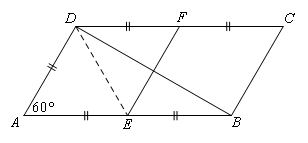
在平行四边形ABCD中,DF//AE,CD=AB,
∵E,F分别为AB,CD的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形ADFE是平行四边形,
∴AD=EF=1cm.
∵AB=2AD,E为AB的中点,
∴AD=AE.
在△ADE中,∠A=60°,
∴△ADE是等边三角形,
∴DE=AE=BE,
∴△ABD是直角三角形,且∠ADB=90°,∠A=60°,
∴BD=![]() =
=![]() .
.
故选D.
略








