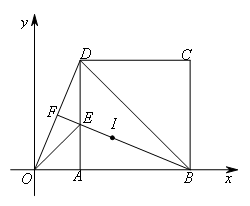
（上接第3，4题）（3）如图，连接OE，点P在直线BF上，若△BPD与△OED相似，则满足条件的点P共有(    )个．

1．解题要点
①△BPD与△OED中，O，E，D，B是定点，△OED是固定的三角形，
首先分析目标三角形中确定的△OED．
②由题意得△OED是等腰三角形，
∵△AOE是等腰直角三角形，
∴∠OEA=45°，
∴∠OED=135°，
∴∠EOD=∠EDO=22.5°，
∴△OED是顶角为135°的等腰三角形．
③由于△BPD中，D，B是定点，
所以首先控制直线BF上的点P，使得△BPD是等腰三角形，
再验证△BPD的顶角是否为135°．
因此首先转化为等腰三角形的存在性（两定一动），再来对结果验证取舍．
2．解题过程
由题意得，△AOE是等腰直角三角形，
∴∠OEA=45°，
∴∠OED=135°，
∴∠EOD=∠EDO=22.5°，
∴△OED是顶角为135°的等腰三角形．
①如图，以点B为圆心，BD长为半径作圆，交直线BF于点，

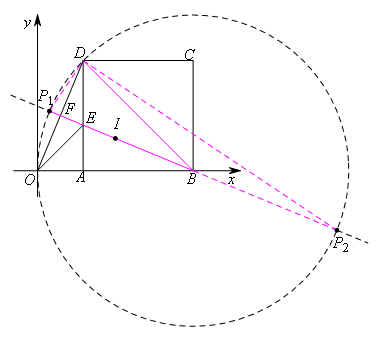
此时△BPD是等腰三角形．
是顶角为22.5°的等腰三角形，不符合条件；
是顶角为157.5°的等腰三角形，也不符合条件．
即此时的不能满足△BPD与△OED相似．
②如图，以点D为圆心，DB长为半径作圆，交直线BF于另一点，

此时是等腰三角形．
∵，
∴，
∴是顶角为135°的等腰三角形，符合条件，
即此时的点满足△BPD与△OED相似．
③如图，作线段BD的垂直平分线，交直线BF于点，

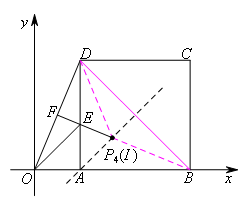
∵BF为线段DO的垂直平分线，
∴点I与点重合，
容易得到是顶角为135°的等腰三角形，符合条件．
即此时的点满足△BPD与△OED相似．
综上所述，满足条件的点P共有2个．

略