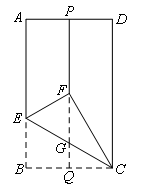
如图,在矩形ABCD中,P,Q分别是边AD,BC的中点,沿过点C的直线折叠矩形ABCD,使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G.若BC的长为3,则线段FG的长为( )
- A.2
- B.
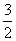
- C.
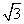
- D.
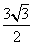
答案
正确答案:C
∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC且AD=BC.
∵P,Q分别是边AD,BC的中点,
∴AP=BQ,AP∥BQ,
∴四边形ABQP为矩形,AB∥PQ,PQ⊥BC,
∴G为CE的中点,△CQF为直角三角形.
如图,由折叠可知,∠1=∠2,∠B=∠EFC=90°,BC=CF.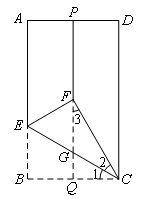
∵Q是BC的中点,
∴![]() ,
,
∴∠3=30°,
∴∠FCQ=60°,
∴∠1=∠2=30°.
在Rt△BCE中,∵∠1=30°,BC=3,
∴![]() ,
,
∴![]() .
.
略








