如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A，C的坐标分别为（10，0），（0，4），D是OA的中点，P是BC边上一点．若△ODP是腰长为5的等腰三角形，则满足条件的点P有(    )

先分析定点、动点，O，D是定点，且OD=5；P是BC边上的动点．
属于等腰三角形存在性中，两定一动的情形．
先找到使得△ODP是等腰三角形的点P，再验证腰长是否为5．
作出两圆，找到圆与线段BC的交点，如图，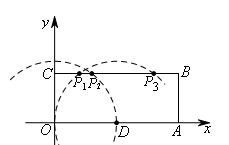

都满足△ODP是腰长为5的等腰三角形．
再作出垂直平分线，如图，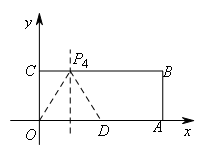

若，则为等边三角形，显然不成立（等边三角形的高与OC不相等）．
综上，符合题意的点P有3个，故选C．

略