已知四边形ABCD的两条对角线AC与BD互相垂直，则下列结论正确的是(    )

选项A：对角线AC与BD互相垂直，AC=BD时，无法得出四边形ABCD是矩形，如图，

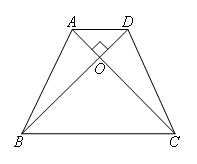
故此选项错误；
选项B：当AB=AD，CB=CD时，无法证明四边形ABCD是菱形，如图，

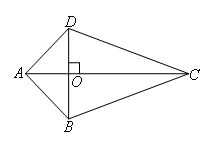
故此选项错误；
选项C：如图，

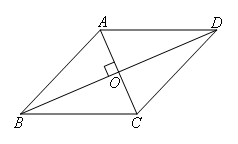
当两条对角线AC与BD互相垂直，AB=AD=BC时，
∴BO=DO，AO=CO，
∴四边形ABCD是平行四边形，
又∵AC⊥BD
∴平行四边形ABCD是菱形，故此选项正确；
选项D：当AC=BD，AD=AB时，无法得到四边形ABCD是正方形，如图，

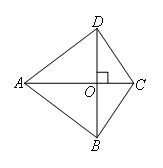
故此选项错误；
故选C．

略