如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
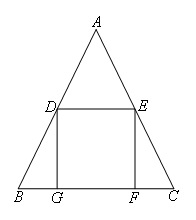
- A.
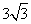 cm
cm - B.4cm
- C.
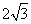 cm
cm - D.
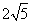 cm
cm
答案
正确答案:D
知识点:等腰三角形的性质 勾股定理 三角形中位线定理 正方形的性质
∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∴![]() ,
,
∵DE=2,
∴BC=4,
∵AB=AC,
∴DB=EC,
在正方形DEFG中,
DG=EF,∠DGF=∠EFG=90°,
∴∠DGB=∠EFC=90°,
∴△BDG≌△CEF(HL),
∴BG=CF=1,
∴![]() ,
,
∴![]() .
.
故选D.
略








