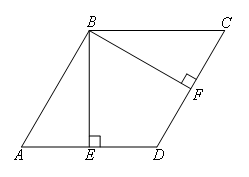
如图，菱形ABCD中，BE⊥AD，BF⊥CD，E，F为垂足，AE=ED，则∠EBF的度数为（    ）

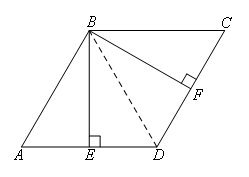
连接BD．
在菱形ABCD中，
AB=AD=CB=CD，
又∵BE⊥AD，AE=ED，
∴BD=AB，
∴△ABD是等边三角形，
∴∠A=60°，
又∵BE⊥AD，BF⊥CD，
∴∠D+∠EBF=180°，
又∵∠D+∠A=180°，
∴∠EBF=∠A=60°．
故选B．

略