如图为等边三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为( )
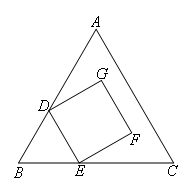
- A.2
- B.3
- C.
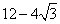
- D.
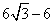
答案
正确答案:D
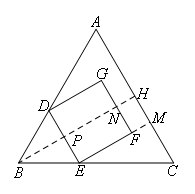
如图,过点B作BH⊥AC于点H,分别交DE,GF于P,N,延长EF交AC于点M,
在等边三角形△ABC中,
∠A=∠ABC=60°,BH⊥AC,
∵BD=BE,
∴△BDE是等边三角形,
∴BP⊥DE,∠BDE=60°,
∴AC∥DE,
在正方形DEFG中,
DE⊥EF,FG∥DE,
∴BH∥EM,AC∥DE∥GF,
∴FM⊥AC,
FM即为F点到AC的距离,
∴四边形PEFN,NFMH均为矩形,
∵AC=18,GF=6,
∴![]() ,
,![]() ,PN=6,
,PN=6,
∴![]() ,
,
故选D.
略








