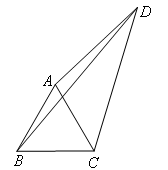
如图,在四边形ABCD中,已知△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则CD的长为( )
- A.
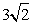
- B.4
- C.

- D.4.5
答案
正确答案:B
1.解题要点
题目中条件比较发散(给出的线段长3和5,与要求的CD长无法联系到一起),但是题目当中给出了等边三角形,就有共顶点的两条相等的线段,那么就可以考虑用旋转来解决问题.
2.解题过程
如图,以CD为边作等边三角形CDE,连接AE.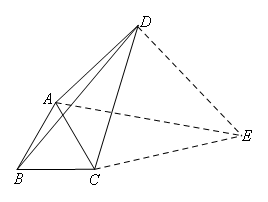
∵∠BCD=∠BCA+∠ACD=∠DCE+∠ACD=∠ACE,
BC=AC,CD=CE,
∴△BCD≌△ACE,
∴BD=AE=5.
又∵∠ADC=30°,
∴∠ADE=90°.
在Rt△ADE中,AE=5,AD=3,
∴DE=4.
∴CD=4.故选B.
略








