(上接第1题)(2)引申拓展
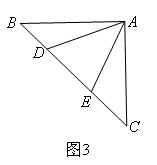
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在BC边上,且∠DAE=45°,则BD,DE,EC之间的数量关系为( )
- A.DE=BD+EC
- B.

- C.
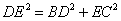
- D.
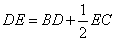
答案
正确答案:C
知识点:中考数学几何中的类比探究
如图,过点A作AG⊥AE,且使得点B,G在AE的同侧,AG=AE,
连接BG,DG.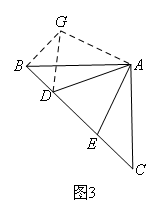
∵∠GAE=∠BAC=90°,
∴∠BAG=∠CAE.
∵AB=AC,AG=AE,
∴△ABG≌△ACE(SAS),
∴BG=CE,∠ABG=∠ACE.
∵∠BAC=90°,AB=AC,∠DAE=45°,
∴∠ABC=∠ACB=∠ABG=45°,∠BAD+∠CAE=45°,
∴∠ABG+∠ABD=∠GBD=90°,∠BAG+∠BAD=∠DAG=45°,
∴∠DAG=∠DAE.
∵AG=AE,AD=AD,
∴△GAD≌△EAD,
∴DG=DE.
在Rt△GBD中,由勾股定理得,![]() ,
,
∴![]() .
.
略








