在等腰△ABC中,∠ACB=90°,且AC=2.过点C作直线 ∥AB,P为直线l上一点,
∥AB,P为直线l上一点,
且AP=AB.则点P到BC所在直线的距离是( )
- A.1
- B.1或
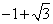
- C.
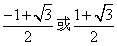
- D.
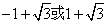
答案
正确答案:D
如图所示,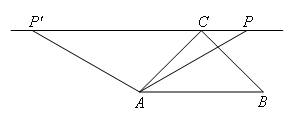
在确定点P位置的时候,以点A为圆心,AB的长为半径作圆,交![]() 于两点,故存在两种情况:
于两点,故存在两种情况:
①求点P到直线BC的距离,如图,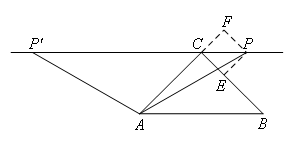
过点P作BC的垂线,垂足为点E;
作AC的垂线,垂足为点F.
则PE=PF,且四边形FCEP是正方形.
在Rt△FAP中,根据勾股定理可得,![]() ,解得
,解得![]() .
.
②求点![]() 到直线BC的距离,如图,
到直线BC的距离,如图,
过点![]() 作BC的垂线,垂足为E;
作BC的垂线,垂足为E;
作AC的垂线,垂足为F.
则![]() ,且四边形
,且四边形![]() 是正方形.
是正方形.
在Rt△![]() 中,根据勾股定理可得,
中,根据勾股定理可得,![]() ,解得
,解得![]() .
.
∴点P到直线BC的距离是![]() .
.
故选D.
略







