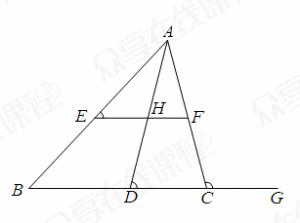
如图：在△ABC中，EF∥BC，∠A的平分线交EF于H，交BC于点D，记∠ADC=α，∠ACB的一个邻补角为β，∠AEF=γ.则α、β、γ的关系是（ ）
- A.α-β=γ
- B.2α-β=γ
- C.3α-β=γ
- D.4α-β=γ
答案
正确答案：B
知识点：平行线的性质 三角形的角平分线、中线和高 三角形的外角性质
∵EF∥BC
∴∠ABC=∠AEF=γ
由三角形的外角等于不相邻的两个内角的和可知：
∠ADC=∠ABC+∠BAD=γ+∠BAD =α
∠ACG=∠ADC+∠DAC=α+∠DAC=γ+∠BAD +∠DAC =β
∵AD平分∠BAC
∴∠BAD =∠DAC=α-γ
∴γ+2(α-γ)= β
即2α-β=γ
略
WORD格式（
