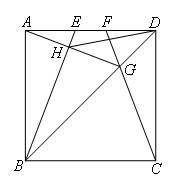
如图,E,F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于点G,
连接BE交AG于点H.若正方形的边长为2,则线段DH的最小值是( )
- A.2
- B.
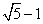
- C.
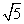
- D.
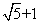
答案
正确答案:B
知识点:三角形三边关系 直角三角形斜边上的中线 正方形的性质 几何最值问题
如图,取AB的中点M,连接MH,MD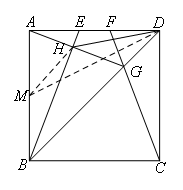
在正方形ABCD中,AB=AD=DC=2,∠BAD=∠CDA=90°,BD为对角线
∴∠ADG=∠CDG
∵DG=DG
∴△ADG≌△CDG(SAS)
∴∠DAG=∠DCG
∵AE=DF
∴△BAE≌CDF(SAS)
∴∠ABE=∠DCG
∴∠ABE=∠DAG
∴∠ABE+∠BAG=∠DAG +∠BAG =90°
∴∠AHB=90°
在Rt△AHB中,M为AB中点
∴![]()
在Rt△AMD中,AD=2,AM=1
∴![]()
此时在△DHM中,![]()
当D,H,M三点共线时,DH的长度最小,其值为![]() .
.
略








