如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

- A.
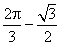
- B.
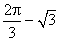
- C.
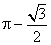
- D.
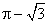
答案
正确答案:B
知识点:菱形的性质 全等三角形的判定与性质 扇形面积的计算
1.解题要点
①要求阴影部分的面积,阴影部分的面积是不规则的,观察图形,用大减小来计算,
连接BD,如图所示,
![]() ;
;
②扇形的面积可以用扇形面积计算公式![]() 来求,四边形BHDG可以进行转化,易得△ABG≌△DBH,则四边形BHDG的面积等于△ABD的面积;△ABD是等边三角形,面积可以用
来求,四边形BHDG可以进行转化,易得△ABG≌△DBH,则四边形BHDG的面积等于△ABD的面积;△ABD是等边三角形,面积可以用![]() 来求.
来求.
2.解题过程
如图,连接BD,设AD,BE相交于点G,设BF,DC相交于点H.
∵四边形ABCD是菱形,∠A=60°,
∴∠ADC=120°,
∴∠1=∠2=∠A=60°,
∴△DAB是等边三角形.
∵AB=2,
∴BD=AB=2.
∵∠4+∠5=60°,∠3+∠4=60°,
∴∠3=∠5,
∴△ABG≌△DBH(ASA).
∴四边形BHDG的面积等于△ABD的面积.
∴![]() .
.
故选B.
略








