如图,在平面直角坐标系中,点A的坐标为(2,0),以OA为边在第四象限内作等边三角形AOB,C为x轴正半轴上的一动点(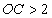 ),连接BC,以BC为边在第四象限内作等边三角形CBD,直线DA交y轴于点E.则点E的坐标为( )
),连接BC,以BC为边在第四象限内作等边三角形CBD,直线DA交y轴于点E.则点E的坐标为( )

- A.
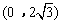
- B.(0,2)
- C.

- D.(0,4)
答案
正确答案:A
∵△OAB与△BCD均为等边三角形,
∴OB=AB,∠OBA=∠OAB=∠AOB=60°,BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,
∴△OBC≌△ABD(SAS),
∴∠BAD=∠BOC=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°.
在Rt△AOE中,∠OAE=60°,OA=2,
∴![]() ,
,
∴点E的坐标为![]() .
.
故选A.
略








