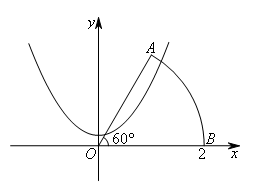
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,
点B的坐标为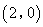 ,扇形的圆心角是60°,若抛物线
,扇形的圆心角是60°,若抛物线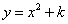 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数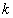 取值范围是( )
取值范围是( )
- A.

- B.
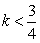
- C.
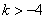
- D.
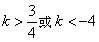
答案
正确答案:A
知识点:数形结合思想
1.解题要点
如图,将抛物线上下平移,可知,
联立![]() 与直线OA的解析式,得抛物线与扇形OAB的边界有一个公共点时
与直线OA的解析式,得抛物线与扇形OAB的边界有一个公共点时![]() 的最大值;抛物线过点B时,得抛物线与扇形OAB的边界有一个公共点时
的最大值;抛物线过点B时,得抛物线与扇形OAB的边界有一个公共点时![]() 的最小值,如图,
的最小值,如图,

故抛物线与扇形OAB的边界总有两个公共点时![]() 的值应在这两个值之间.
的值应在这两个值之间.
2.解题过程
由题意,![]() ,
,
∴![]() ,
,
∴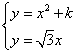 ,可得:
,可得:![]() .
.
令![]() ,解得:
,解得:![]() ,
,
∴![]() 时抛物线与扇形OAB有一个公共点.
时抛物线与扇形OAB有一个公共点.
当抛物线过点![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() 时抛物线与扇形OAB的边界有一个公共点.
时抛物线与扇形OAB的边界有一个公共点.
∴![]() 时抛物线
时抛物线![]() 与扇形OAB的边界总有两个公共点.
与扇形OAB的边界总有两个公共点.
故选A.
略








