已知:如图,∠1=∠2,∠A=∠C.
求证:AE∥BC.
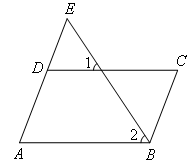
证明:如图,
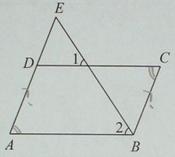
∵∠1=∠2(已知)
∴AB∥CD( )
∴∠A=∠CDE( )
∵∠A=∠C(已知)
∴∠C=∠CDE(等量代换)
∴ ( )
①同位角相等,两直线平行;②两直线平行,同位角相等;③AB∥CD;④AE∥BC;
⑤两直线平行,内错角相等;⑥内错角相等,两直线平行.
以上空缺处依次所填正确的是( )
- A.②①④⑥
- B.②①④⑤
- C.①②④⑥
- D.①②③⑥
答案
正确答案:C
第一个空:条件是∠1=∠2,其中∠1和∠2是同位角,结论是AB∥CD,由同位角相等得到两直线平行,理由是①同位角相等,两直线平行;
第二个空:条件是AB∥CD,结论是∠A=∠CDE,而∠A与∠CDE为同位角,由两直线平行得到同位角相等,理由是②两直线平行,同位角相等;
第三个空:条件是∠C=∠CDE,其中∠C和∠CDE是内错角,结论应为④AE∥BC,由内错角相等得到两直线平行,理由是⑥内错角相等,两直线平行.
故选C.
略









