已知A,B两港口相距150海里,甲船从A港行驶到B港后,休息一段时间,速度不变,沿原航线返回,同时,乙船从A港出发驶向B港,甲、乙两船离A港的距离s(海里)与甲船行驶时间t(小时)之间的函数关系如图所示.当两船相遇时,两船到A港的距离为90海里,乙船在行驶过程中,速度不变,则甲船行驶( )小时后,两船在甲船返航过程中相距30海里.(假设甲、乙两船沿同一航线航行)

- A.
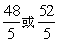
- B.
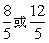
- C.10
- D.
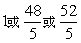
答案
正确答案:A
知识点:一次函数应用题
根据图象可得,OC段表达式为:![]() ,
,
∵甲船休息后返航速度不变,
∴DM段的斜率为-30,
结合D点坐标可得DM段表达式为:![]() .
.
∵两船相遇时距离A港90海里,
∴G点纵坐标为90,代入s=-30t+390得:t=10,
即G点坐标为(10,90),
结合E点坐标可得EF段表达式为:![]() .
.
两船相距30海里,在图象上的表现即为:![]() ,
,
∴-30t+390-(45t-360)=30或45t-360-(-30t+390)=30,
解得:![]() .
.
故选A.
略








