已知一次函数y=ax+b,当 时,对应的函数值y的取值范围是
时,对应的函数值y的取值范围是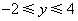 ,则ab的值为( )
,则ab的值为( )
- A.12
- B.-6
- C.-6或-12
- D.6或12
答案
正确答案:C
知识点:待定系数求表达式
当a![]() 0时,即y=ax+b单调递增时,
0时,即y=ax+b单调递增时,
函数过(0,-2),(2,4)两个点,
得y=3x-2
即a=3,b=-2
∴ab=-6
当a![]() 0时,即y=ax+b单调递减时,
0时,即y=ax+b单调递减时,
函数过(0,4),(2,-2)两个点,
得y=-3x+4
即a=-3,b=4
∴ab=-12
综上ab=-6或-12.
故选C
略







