如图,在△ABC中,AB=AC,AD=DE,∠BAD=20°,∠EDC=10°,则∠DAE的度数为( )
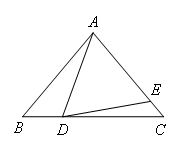
- A.30°
- B.40°
- C.60°
- D.80°
答案
正确答案:C
知识点:等腰三角形的性质
分析:题目中涉及到的角度比较多,由于等腰,相等的角也多,
因此可以通过设角度来表达其他角.可以设∠B=α,表达出其他角,
把角度往△ADE中转,然后利用三角形内角和进行计算.
过程示范:
设∠B=α
∵AB=AC
∴∠B=∠C=α
∵∠ADC是△ABD的一个外角
∴∠ADC=∠B+∠BAD
∵∠BAD=20°
∴∠ADC=α+20°
∵∠EDC=10°
∴∠ADE=α+20°-10°=α+10°
∵∠AED是△CDE的一个外角
∴∠AED=∠C+∠EDC=α+10°
∵AD=DE
∴∠DAE=∠AED=α+10°
∴α+10°+α+10°+α+10°=180°
∴α=50°
∴∠DAE=α+10°=60°
故选C.
略








