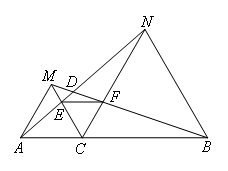
如图，点C为线段AB上一点，△ACM，△CBN是等边三角形，AM=AC=CM，BC=CN=BN，∠ACM=∠BCN=60°，连接AN交CM于点E，连接BM交CN于点F，且AN与BM交于点D．则下列结论错误的是(    )

解：如图，
∵∠ACM=∠BCN
∴∠ACM+∠ECF=∠BCN+∠ECF
即∠ACN=∠MCB
在△CAN和△CMB中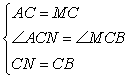

∴△CAN≌△CMB（SAS），故A选项正确；
∴∠CNE=∠CBF
∵∠ACM=∠BCN=60°
∠ACM+∠BCN+∠ECN=180°
∴∠ECN=∠BCN=60°
在△CEN和△CFB中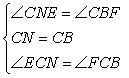

∴△CEN≌△CFB（ASA），故B选项正确；
∴CE=CF
∵∠ECN=60°
∴△CEF为等边三角形，故C选项正确；
∵∠NDF是△ADB的一个外角
∴∠NDF=∠DAB+∠DBA
∵∠DBA=∠CNE
∴∠NDF=∠DAB+∠CNE
∵∠NCB是△ACN的一个外角
∴∠NCB=∠DAB+∠CNE
∴∠NDF=∠NCB
∵∠NCB=60°
∴∠NDF=60°，故D选项错误．
故选D．

略