如图，在Rt△ABC中，∠ACB=90°，CF⊥AB于点F，BD平分∠ABC，且交CF于G，DE⊥AB于点E，则下列结论不一定正确的是(    )

解：如图，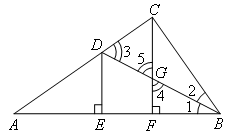

A选项：
∵∠ACB=90°
∴∠A+∠ABC=90°
∵CF⊥AB
∴∠CFB=90°
∴∠BCF+∠ABC=90°
∴∠A=∠BCF，故A选项正确；
B选项：
由DE⊥AB，∠ACB=90°，BD平分∠ABC
得DE=DC
在Rt△BCD和Rt△BED中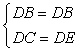

∴Rt△BCD≌Rt△BED（HL）
∴BC=BE，故B选项正确．
C选项：
通过题中条件，不能判定△ADE是否全等于△BDE，
因此不能判定AD是否等于BD，故C选项错误；
D选项：
∵BD是∠ABC的平分线
∴∠1=∠2
∵CF⊥AB
∴∠GFB=90°
∴∠1+∠4=90°
∴∠2+∠4=90°
∵∠ACB=90°
∴∠2+∠3=90°
∴∠3=∠4
∵∠4=∠5
∴∠3=∠5
即∠CDG=∠CGD，故D选项正确．
综上，故选C．

略