1编号:85599题型:单选题测试正确率:0%
已知:如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,
∠BDC=90°,BD=CD,CE与BD交于F,连接AF.
求证:CF=AB+AF.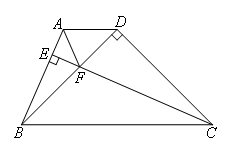
证明:如图, 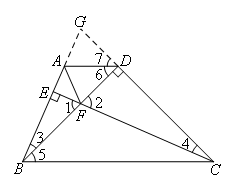
∵△BDC为等腰直角三角形
∴∠GDB=∠BDC=90°,∠5=45°,BD=CD
∵CE⊥AB
∴∠CEB=90°
∴∠1+∠3=90°,∠2+∠4=90°
∵∠1=∠2
∴∠3=∠4
在△GBD和△FCD中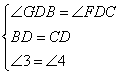
∴△GBD≌△FCD(ASA)
∴
∴∠6=∠7
在△GDA和△FDA中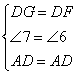
∴△GDA≌△FDA(SAS)
请你仔细观察下列序号所代表的内容:
①延长BA交CD的延长线于点G;②延长BA到G使AG=AF,连接DG;
③BG=CF,DG=DF;④BG=CF,∠G=∠2;⑤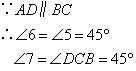 ;
;
⑥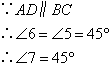 ;⑦
;⑦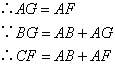 ;⑧
;⑧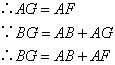 .
.
以上空缺处依次所填最恰当的是( )
2编号:85598题型:单选题测试正确率:0%
3编号:85597题型:单选题测试正确率:0%
4编号:85596题型:单选题测试正确率:0%
5编号:85454题型:单选题测试正确率:0%
6编号:85452题型:单选题测试正确率:0%
7编号:59927题型:单选题测试正确率:0%
已知:如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,
∠BDC=90°,BD=CD,CE与BD交于F,连接AF.
求证:CF=AB+AF.
证明:如图, 
∵△BDC为等腰直角三角形
∴∠GDB=∠BDC=90°,∠5=45°,BD=CD
∵CE⊥AB
∴∠CEB=90°
∴∠1+∠3=90°
∠2+∠4=90°
∵∠1=∠2
∴∠3=∠4
在△GBD和△FCD中
∴△GBD≌△FCD(ASA)
∴
∴∠6=∠7
在△GDA和△FDA中
∴△GDA≌△FDA(SAS)
请你仔细观察下列序号所代表的内容:
①延长BA交CD的延长线于点G;②延长BA到G使AG=AF,连接DG;
③BG=CF,DG=DF;④BG=CF,∠G=∠2;⑤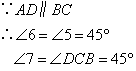 ;
;
⑥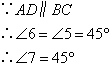 ;⑦
;⑦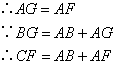 ;⑧
;⑧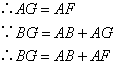 .
.
以上空缺处依次所填最恰当的是( )
8编号:59926题型:单选题测试正确率:0%
9编号:59925题型:单选题测试正确率:0%
已知:如图,在四边形ABCD中,AD∥BC,点E是CD的中点,连接AE,BE,且AE⊥BE.
求证:AB=AD+BC.

证明:如图,

∵AD∥BC
∴∠D=∠1
∵E是CD的中点
∴DE=CE
在△ADE和△FCE中

∴△ADE≌△FCE( )
∴
∵AE⊥BE
∴∠AEB=∠FEB=90°
在△AEB和△FEB中

∴△AEB≌△FEB( )
请你仔细观察下列序号所代表的内容:
①延长AE到F,使EF=AE,连接CF;②延长AE交BC的延长线于点F;③ASA;④SAS;⑤AAS;
⑥AE=FE;⑦AE=FE,AD=FC;⑧ ;⑨
;⑨ .
.
以上空缺处依次所填最恰当的是( )
10编号:59924题型:单选题测试正确率:0%