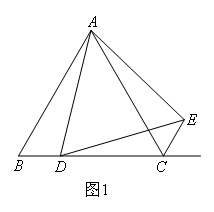
如图，△ABC是等边三角形，边长为2，点D在线段BC上（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．当四边形ADCE的周长取最小值时，BD的长为____．

∵△ABC是等边三角形，
∴AB=AC，
∵∠DAE=∠BAC，
∴∠BAD=∠CAE，
∵AD=AE
∴△ABD≌△ACE（SAS）
BD=CE
C_{四边形ADCE}=AD+DC+CE+AE
=AD+DC+BD+AE
=2AD+BC
当AD⊥BC时，四边形ADCE的周长取得最小值，
结合等边三角形的性质，可知，此时∠BAD=30°，
所以BD=1

略