已知:如图,AB=AE,BC=DE,∠B=∠E,F是CD的中点.
求证:∠BAF=∠EAF.
下面是小明的几种思路,其中正确的是( )
- A.连接AC,AD,先证明△ACF≌△ADF,再证明△ABC≌△AED,得∠BAF=∠EAF
- B.连接AC,AD,先证明△ABC≌△AED,再证明△ACF≌△ADF,最后可得∠BAF=∠EAF
- C.连接BF,EF,直接证明△ABF≌△AEF,得∠BAF=∠EAF
- D.连接BF,EF,先证明△BCF≌△EDF,再证明△ABF≌△AEF,得∠BAF=∠EAF
答案
正确答案:B
知识点:全等三角形的性质 全等三角形的判定 全等三角形之辅助线
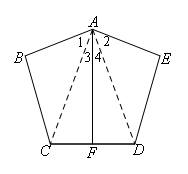
观察图形,题中已知AB=AE,BC=DE,∠B=∠E,
因此连接AC,AD,即可得到△ABC≌△AED(SAS),
由全等可以得到∠1=∠2,AC=AD;
结合要求的结论,题中点F是CD的中点,则CF=DF,
进而得到△ACF≌△ADF(SSS),由全等可以得到∠3=∠4,
所以∠1+∠3=∠2+∠4,即∠BAF=∠EAF.
注意:不考虑连接BF,EF,这样会破坏已知条件∠B=∠E,
故选B.
略








