如图,△ABC是边长为1的等边三角形,P是△ABC内任意一点,过点P作EF∥AB交AC、BC于点E、F,作GH∥BC交AB,AC于点G、H,作MN∥AC交AB、BC于点M、N,请你猜想EF+GH+MN的值是否随点P位置(P点在△ABC内)的变化而变化,若变化,说明理由;若不变化,请求出它的值.

答案
解:EF+GH+MN的值不随点P位置的变化而变化,且EF+GH+MN=2.
理由如下:如图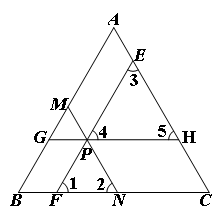
在等边△ABC中,∠A=∠B=∠C=60°,AB=AC=BC=1
∵EF//AB,MN//AC,GH//BC
∴四边形AMPE是平行四边形
且∠1=∠B=60°,∠2=∠C=60°,∠5=∠C=60°,
∠3=∠A=60°,∠4=∠1=60°=∠5=∠3
∴∠1=∠C,∠2=∠B,△EPH是等边三角形,
同理△MPG是等边三角形
∴MN=MB,EF=EC,PH=EP=AM,PG=PM=AE
∴EF+GH+MN=EC+PH+PG+MB=EC+AM+AE+MB=AC+AB=2.
知识点:线段间的关系
略
略








