在正方形ABCD中，点P是CD上一动点，连接PA，分别过点B、D作BE⊥PA、DF⊥PA，垂足分别为E、F．（1）如图1，请探索BE、DF、EF这三条线段长度具有怎样的数量关系．直接写出结论．（2）若点P在DC的延长线上（如图2），那么这三条线段的长度之间又具有怎样的数量关系，并证明．（3）若点P在CD的延长线上呢（如图3）？请分别直接写出结论并简要说明理由．
答案
解：（1）BE=DF+EF；
（2）BE=DF-EF，理由如下：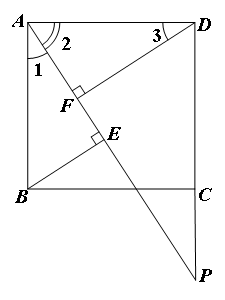
在正方形ABCD中，AB=AD，∠BAD=90°
即∠1+∠2=90°
∵BE⊥AP，DF⊥AP
∴∠2+∠3=90°
∴∠1=∠3
在△ABE和△DAF中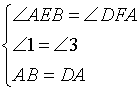
∴△ABE≌△DAF（AAS）
∴AE=DF，BE=AF
∴BE=AF=AE-EF=DF-EF.
（3）BE=EF-DF，提示：可证△ABE≌△DAF，BE=AF=EF-AE=EF-DF.
知识点：线段间的关系
略
略
WORD格式（
