己知:正方形ABCD.(1)如图1,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系和位置关系分别是什么?请直接写出结论.(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,猜想线段AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.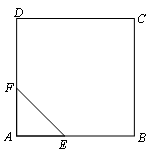
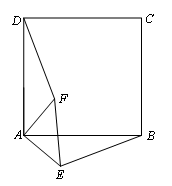
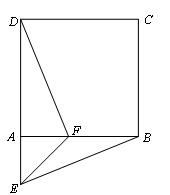
图1 图2 图3
答案
解:(1)BE=DF且BE⊥DF;
(2)(1)中结论仍成立在△DFA和△BEA中,
∵∠DAF=90°-∠FAB,∠BAE=90°-∠FAB,
∴∠DAF=∠BAE,又AB=AD,AE=AF,
∴△DFA≌△BEA,
∴BE=DF;∠ADF=∠ABE,延长DF交AB于M,交BE于N
∵∠ADF+∠DMA=90°,∠DMA=∠BMN
∴∠ABE+∠BMN=90°
∴∠MNB=90°即BE⊥DF
BE=DF,BE⊥DF仍成立
(3)AE=(![]() -1)AD;
-1)AD;
知识点:图形的旋转
略
略










