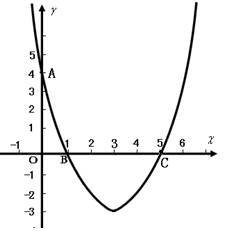
如图，在平面直角坐标系xoy中，已知抛物线经过点A(0，4)，B(1，0)，C（5，0），抛物线对称轴l与x轴相交于点M．
（1）求抛物线的解析式和对称轴；
（2）设点P为抛物线（x＞5）上的一点，若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数，请你直接写出点P的坐标；
（3）连接AC．探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请你说明理由．
答案
解：（1）根据已知条件可设抛物线的解析式为y=a（x-1）（x-5），
把点A（0，4）代入上式得：
,
∴
，
∴抛物线的对称轴是：x=3．
（2）由已知，可求得P（6，4）．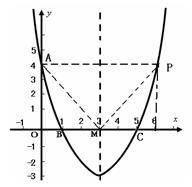
提示：由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3，
又知点P的坐标中x＞5，所以，MP>2,AP>2；
因此以1、2、3、4为边或以2、3、4、5为边都不符合题意，
所以四条边的长只能是3、4、5、6的一种情况，
在Rt△AOM中，
，
因为抛物线对称轴过点M，
所以在抛物线x＞5的图象上有关于点A的对称点与M的距离为5，
即PM=5，此时点P横坐标为6，即AP=6；
故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立，即P（6，4）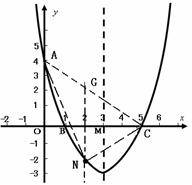
（3）法一：在直线AC的下方的抛物线上存在点N，使△NAC面积最大．
设N点的横坐标为
，此时点N
（
，
过点N作NG∥y轴交AC于G；由点A（0，4）和点C（5，0）
可求出直线AC的解析式为：
；
把x=t代入得：
，则G
，
此时：
∴
∴当
时，△CAN面积的最大值为
，
由，得：
，
∴N（
，-3）
法二：提示：过点N作x轴的平行线交
轴于点E，
作CF⊥EN于点F，则
（再设出点N的坐标，同样可求,余下过程略）
知识点：二次函数综合题
1．在第二问中要确定P点坐标，考虑到AO=4、OM=3，所以可以初步对剩下两条边的范围做一个限制，又由于MP＞2,AP＞2,那么必然只能是3、4、5、6这唯一的一种情况；2．在表达△NAC面积时，虽然不是一个特殊的三角形，但是A、C两点是固定的，也就是说这条直线是固定的，要在抛物线上找一个点使三角形面积最大，那么就可以做对称轴的垂线，把三角形分割成两个易求的三角形的面积进行表达，进而求出面积的最大值；
1．在第二问中对于题目理解不清楚，不知道连续4个正整数如何去做，也就是不能找到固定线段的长度；
2．确定范围之后不能很好判定范围，主要根据已有线段进行判断；
3．在最后一问求面积的时候，对于非特殊三角形的面积，不能转化为特殊三角形的面积．
WORD格式（
