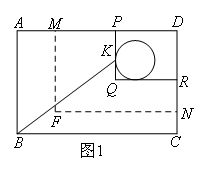
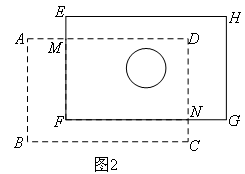
一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上.木工师傅想了一个巧妙的办法,他通过测量得到以下数据:BC=130cm,PD=50cm,DR=40cm,RC=44cm,PQ与圆洞的切点K到点B的距离为100cm,从点N沿折线NF-FM(NF∥BC,FM∥AB)切割,如图1所示.图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠,无缝隙,不记损耗),则CN,AM的长分别是( )

A.18cm,36cm
B.31cm,18cm
C.15cm,30cm
D.18cm,31cm

答案

正确答案：D

如图所示，设圆心为O，连接OF，OK，延长OK交线段MF于点S，交AB于T，

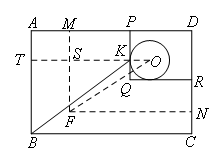
由拼接之后的图形可知，矩形和圆都关于此圆圆心中心对称.
则SF=AB=(DR+RC)=42cm,OS=BC=65cm,
在Rt△BTK中，TK=BC-PD=130-50=80(cm)，BT=60cm；
KQ=BT-RC=60-44=16(cm)，即圆的半径为16cm，
则AT=DR-KQ=40-16=24(cm),
设AM=m cm，
则OS=TK+OK-AM=80 +16-m=96-m=65，
∴m=31
设CN=n cm，
则SF=AB-AT-CN=84-24-n=60-n=42，
∴n=18

略

下载次数：2

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>