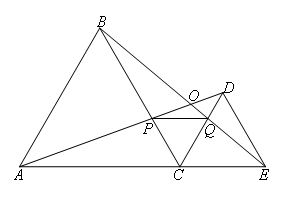
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和
正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.有下列结论:①AD=BE;②AP=BQ;
③∠AOB=60°;④DE=DP,其中正确的结论有(    )

1．思路点拨
对于多结论问题，需要我们注意两点：第一，需要对每一个结论一一进行验证，第二，已经证明出来的结论，可以作为条件证明其他结论.
根据等边三角形性质得出AC=BC，DC=CE，∠BCA=∠DCE=60°，求出∠ACD=∠BCE，证明
△ACD≌△BCE，推出AD=BE，即可判断①；根据全等三角形性质得出∠CBE=∠CAD，根据
ASA证明△ACP≌△BCQ，推出AP=BQ，即可判断②；求出∠DCE=60°=∠CAD+∠ADC，
求出∠CAD+∠BEC=60°，即可求出∠AOB=60°，即可判断③；根据三角形外角性质推出
∠DPC＞∠DCP，推出DP≠DC，即可判断④．
2．解题过程
结论①
∵△ABC和△DCE是正三角形，
∴AC=BC，DC=CE，∠BCA=∠DCE=60°，
∴∠BCA+∠BCD=∠DCE+∠BCD，
∴∠ACD=∠BCE，
在△ACD和△BCE中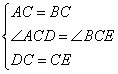

∴△ACD≌△BCE（SAS），
∴AD=BE，
∴①正确；
结论②
∵△ACD≌△BCE，
∴∠CBE=∠CAD，
∵∠ACB=∠DCE=60°，
∴∠BCD=60°=∠ACB，
在△ACP和△BCQ中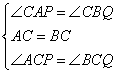

∴△ACP≌△BCQ（ASA），
∴AP=BQ，
∴②正确；
结论③
∵△ACD≌△BCE，
∴∠ADC=∠BEC，
∠DCE=60°=∠CAD+∠ADC，
∴∠CAD+∠BEC=60°，
∴∠AOB=∠CAD+∠BEC=60°，
∴③正确；
结论④
∵△DCE是正三角形，
∴DE=DC，
∵∠AOB=60°，∠DCP=60°，∠DPC＞∠AOB，
∴∠DPC＞∠DCP，
∴DP<DC，即DP≠DE，
∴④错误；
故选A．

略