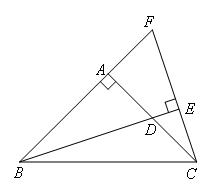
如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于点E,交BA的延长线于点F,若BF=12,则△FBC的面积为(    )

1．思路点拨
（1）由及BF=12可知，关键是求AC的长；
（2）题目有边相等，且直角比较多，可以借助互余转移角，
证明△ABD≌△ACF（AAS或ASA），进而借助全等的性质转移边，得到AD=AF；
（3）结合AC=2AD，
∴AB=2AF，
∴BF=3AF=3AD=12，AD=4，AC=8，
（4）代入公式求解三角形的面积．
2．解题过程
解：∵∠F+∠FBE=90°，∠F+∠FCA=90°
∴∠FBE=∠FCA
在Rt△BAD和Rt△CAF中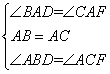

∴Rt△BAD≌Rt△CAF（ASA）
∴AD=AF
∵D是AC的中点
∴AC=2AD
∵AB=AC
∴AB=2AD=2AF
∴BF=3AF=3AD=12
∴AD=4，AC=2AD=8
∴，选C
3．易错点
①不能根据图形发现全等三角形，设计方案求解AC的长；
②发现全等之后，不能发现线段之间的倍数关系，求解线段长．

略