如图,直线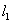 ∥
∥ ,⊙O与
,⊙O与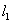 和
和 分别相切于点A和点B.点M和点N分别是
分别相切于点A和点B.点M和点N分别是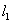 和
和 上的动点,
上的动点,
MN沿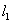 和
和 平移.⊙O的半径为1,∠1=60°,下列结论错误的是( )
平移.⊙O的半径为1,∠1=60°,下列结论错误的是( )
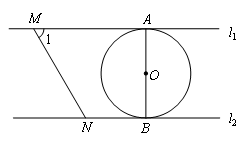
- A.
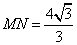
- B.若MN与⊙O相切,则
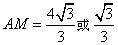
- C.若∠MON=90°,则MN与⊙O相切
- D.
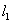 和
和 的距离为2
的距离为2
答案
正确答案:B
如图,过点N作![]() ,垂足为C,
,垂足为C,
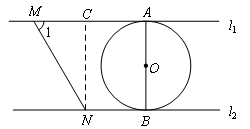
则NC∥AB.
∵![]() ∥
∥![]() ,
,
易知四边形ACNB为矩形,
∴CN=AB=2,∠NCM=90°.
∵∠1=60°,
∴∠CNM=30°,
∴![]() ,
,
∴选项A中结论正确,不符合题意.
当MN与⊙O相切时,容易发现在AB两侧各有一个位置,如图所示,
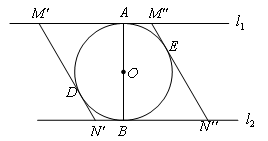
连接![]() ,
,
容易证明![]() ,
,
∴![]() .
.
∵OA=1,
∴![]() .
.
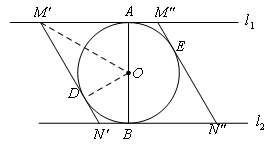
同理可求![]() ,
,
∴当MN与⊙O相切时,![]() ,选项B中结论错误,符合题意.
,选项B中结论错误,符合题意.
当∠MON=90°时(只考虑在AB左侧的情况,右侧同理),如图所示,过点O作OG⊥MN,垂足为G,若要证明MN与⊙O相切,只要证明OG=1即可.
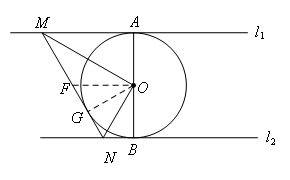
取MN的中点F,连接OF,
则OF=FM,且OF∥AM,
∴∠OMF=∠MOF=∠OMA,
∴Rt△OMG≌Rt△OMA,
∴OG=OA=1,
∴MN与⊙O相切,
即当∠MON=90°,MN与⊙O相切,选项C成立,但是不符合题意.
选项D正确,但是不符合题意.
略








