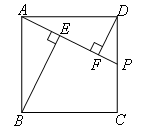
在正方形ABCD中,P是直线CD上一点,连接PA,分别过点B,D作BE⊥PA,DF⊥PA,垂足分别为点E,F.
(1)如图,当点P在边CD上时,BE,DF,EF这三条线段之间的数量关系为(    )

• A.
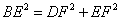
• B.BE=DF-EF
• C.BE=EF-DF
• D.BE=DF+EF

答案

正确答案：D

知识点：全等三角形的性质  全等三角形的判定  正方形的性质  类比探究问题  

∵四边形ABCD为正方形，
∴AB=DA，∠BAD=90°，
∴∠EAB+∠DAF=90°．
∵BE⊥PA，DF⊥PA，
∴∠BEA=∠AFD=90°，
∴∠EAB+∠ABE=∠EAB+∠DAF=90°，
∴∠ABE=∠DAF，
∴△ABE≌△DAF，
∴BE=AF，AE=DF，
∴BE=AE+EF=DF+EF．

略

下载次数：6

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>