如图,在等边三角形ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是( )
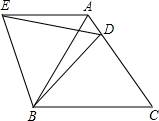
- A.
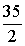
- B.18
- C.19
- D.20
答案
正确答案:C
∵△ABC是等边三角形,
∴AC=AB=BC=10.
∵△BAE由△BCD逆时针旋旋转60°得出,
∴AE=CD,BD=BE,∠EBD=60°,
∴AE+AD=AD+CD=AC=10.
∵∠EBD=60°,BE=BD,
∴△BDE是等边三角形,
∴DE=BD=9,
∴△AED的周长为AE+AD+DE=AC+BD=19.
略








