如图，在Rt△ABC中，∠ABC=90°，D为斜边AC上一点，连接BD．E为BD上一点，过点E作正方形EFGH和正方形EIJK，使得点F，G在BC边上，点H，I在AC边上，点J，K在AB边上．若EF=3，EK=2，则AC的长为(    )

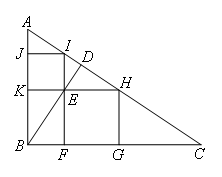
• A.
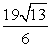
• B.
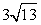
• C.
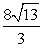
• D.

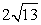
答案

正确答案：A

知识点：勾股定理  正方形的性质  相似三角形的判定和性质  

易得正方形EFGH和正方形EIJK的边长分别为3，2，△CGH∽△CFI，
∴，即，
∴．
同理求得，
∴，．
在Rt△ABC中，由勾股定理得，
．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>