如图,在△ABC中,∠BAC=60°,∠ABC=45°,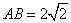 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
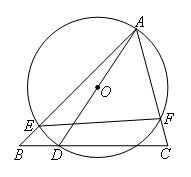
- A.2
- B.
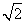
- C.
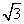
- D.3
答案
正确答案:C
弦EF的长度变化,是由直径AD的变化引起的,在点D运动的过程中,△ABC是固定不动的,除此之外与圆有关的且与EF有关的固定不动的是弦EF所对的圆周角∠BAC(=60°),所以弦EF和直径存在某一固定关系.
如图,延长EO交⊙O于点G,连接GF,
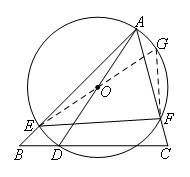
在Rt△EGF中,∠EAF=∠EGF=60°,
∴![]() ,
,
∴AD取最小值时,EF也取最小值.
点A是直线BC外一点,点D是BC上一点,则当AD⊥BC时,AD取最小值(此时情况如图所示).
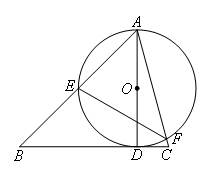
在Rt△ABD中,∠B=45°,![]() ,
,
∴AD=2,
∴![]() ,
,
则EF的最小值为![]() .
.
略








