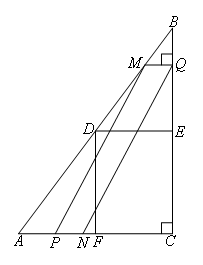
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D,E,F分别是边AB,BC,AC的中点,连接DE,DF.动点P,Q分别从点A,B同时出发,运动速度均为每秒1个单位长度,点P沿A→F→D的方向运动到点D停止;点Q沿BC的方向运动,当点P停止运动时,点Q也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形PMQN与矩形FDEC重叠部分的面积为y(这里规定:线段是面积为0的几何图形),点P运动的时间为x(s).
(1)当点P运动到点F时,CQ的长度为( )
- A.3
- B.4
- C.5
- D.6
答案
正确答案:C
知识点:动点问题
△ABC是三边为6,8,10的直角三角形,
点D,E,F分别为三边中点,
则△BDE和△DAF是三边为3,4,5的直角三角形,且AF=DE=3,BE=DF=4.
由于QM⊥BC,所以△BQM是三边之比为3:4:5的三角形.
在点P从点A运动到点F的过程中,
AP=BQ=x,
当点P运动到点F时,x=3,
∴BQ=3,
∴CQ=BC-BQ=8-3=5.
略








