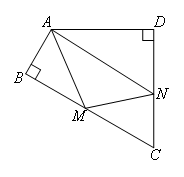
如图，在四边形ABCD中，∠BAD=120°，∠B=∠D=90°．点M，N分别为BC，CD边上的动点，则当△AMN的周长最小时，∠AMN+∠ANM的度数为(    )

如图，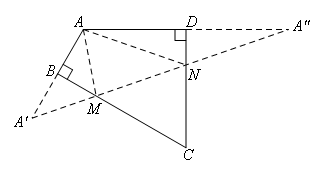

作点A关于BC，CD的对称点A′，A″，连接A′A″，与BC，CD分别交于点M，N，此时△AMN的周长最小．
∵∠BAD=120°，
∴∠A′+∠A″=60°．
由轴对称的性质可知，
∠MAB=∠A′，∠NAD=∠A″，
∴∠MAB+∠NAD=∠A′+∠A″=60°．
∵∠AMN与∠ANM分别是△AMA′与△ANA″的外角，
∴∠AMN=∠MAB+∠A′=2∠A′，∠ANM=∠NAD+∠A″=2∠A″，
∴∠AMN+∠ANM=2（∠A′+∠A″）=120°．
故选B．

略