(上接第4题)(2)若在直线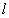 上存在点M,使得△MAC是等腰三角形,则点M的坐标为( )
上存在点M,使得△MAC是等腰三角形,则点M的坐标为( )
- A.(1,6),
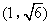 ,
,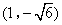 或(1,1)
或(1,1) - B.(1,0),(1,6),
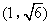 ,
,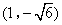
- C.(1,0),
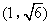 ,
,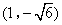 或(1,1)
或(1,1) - D.(1,0),(1,6),
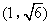 ,
,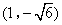 或(1,1)
或(1,1)
答案
正确答案:C
知识点:两圆一线 等腰三角形存在性 二次函数背景下的存在性问题
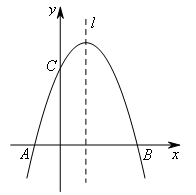
A,C为定点,M为直线![]() 上的动点,
上的动点,
利用两圆一线确定点M的位置,进而求出点M的坐标.
由(1)知抛物线的对称轴为直线x=1,设点M的坐标为(1,m).
如图,以点C为圆心,CA长为半径作圆,交直线![]() 于点
于点![]() ,
,![]() .
.

由CA=CM,得![]() ,即
,即![]() ,
,
∴m=0或m=6.
∵当m=6时,A,C,M三点在同一直线上,不符合题意,
∴此时点M的坐标为(1,0).
如图,以点A为圆心,AC长为半径画圆,交直线![]() 于点
于点![]() ,
,![]() .
.
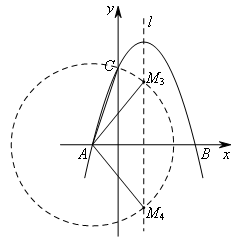
由![]() 得,
得,![]() ,
,
∴![]() ,
,
∴此时点M的坐标为![]() .
.
如图,作线段AC的垂直平分线,交直线![]() 于点
于点![]() .
.
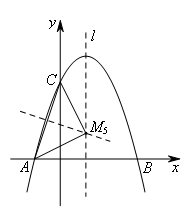
由![]() 得,
得,![]() ,
,
∴m=1,
∴此时点M的坐标为(1,1).
综上得,点M的坐标为(1,0),![]() ,
,![]() 或(1,1).
或(1,1).
略








