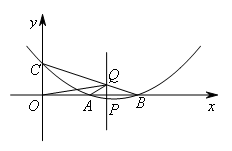
如图,抛物线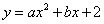 与x轴交于A(3,0),B(6,0)两点,与y轴交于点C.P是抛物线上一点,过点P作PQ∥y轴,交直线BC于点Q.设点P的横坐标为
与x轴交于A(3,0),B(6,0)两点,与y轴交于点C.P是抛物线上一点,过点P作PQ∥y轴,交直线BC于点Q.设点P的横坐标为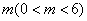 ,当△OAQ为直角三角形时,m的值为( )
,当△OAQ为直角三角形时,m的值为( )
- A.
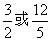
- B.
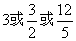
- C.
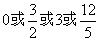
- D.
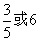
答案
正确答案:B
1.解题要点
①首先研究基本图形,A(3,0),B(6,0),C(0,2)很容易得到,
直线BC的解析式也可以得到;
②分析目标△OAQ,O,A是定点,Q是动点,若△OAQ是直角三角形,需要根据直角顶点进行分类,把三个顶点轮流作直角顶点进行分析;
③对于直角的处理,分类时,应从最简单的入手,可以结合题目背景进行分析排除,如当![]() 时,点O不能作直角顶点,计算时,可以结合题目背景灵活处理.
时,点O不能作直角顶点,计算时,可以结合题目背景灵活处理.
2.解题过程
由题意得,A(3,0),B(6,0),C(0,2),![]() .
.
∵点P的横坐标为m,
∴![]() .
.
①当点O为直角顶点时,显然不成立;
②当点A为直角顶点时,过点A作AQ⊥AB交BC于点Q,点Q满足题意,
此时点P与点A重合,
∴![]() .
.
③当点Q为直角顶点时,如图所示,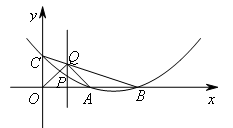
由于只要确定了点Q的位置,就能求出m的值,
抛物线在解题中不发挥作用,将抛物线去掉,如图所示,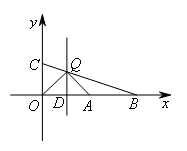
设直线PQ与x轴交于点D.
方法一:利用OQ与AQ垂直,两直线斜率乘积等于-1建等式.
直线OQ的斜率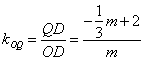 ,
,
直线AQ的斜率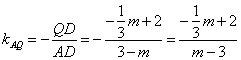 .
.
∵![]() ,
,
∴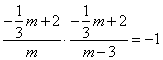 ,
,
化简可得![]() ,
,
解得![]() .
.
方法二:利用直角三角形中射影定理建等式,即![]() .
.
即![]() ,同上可解.
,同上可解.
综上,符合题意的m的值为![]() .
.
略








