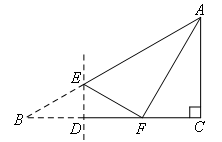
如图，在Rt△ABC中，∠ACB=90°，∠B=30°，BC=6．D是BC边上一动点（不与点B，C重合），过点D作DE⊥BC，交AB于点E，将∠B沿直线DE翻折，点B落在射线BC上的点F处．当△AEF为直角三角形时，BD的长为(    )

由折叠可知∠EFB=∠B=30°，DF=BD，
∴∠AEF=60°．
在Rt△ABC中，∠ACB=90°，∠B=30°，BC=6，
∴，∠BAC=60°．
当∠AFE=90°时，如图1所示，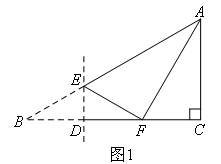

易知∠AFC=60°，
∴CF=2，
∴BD=DF=2．
当∠EAF=90°时，如图2所示，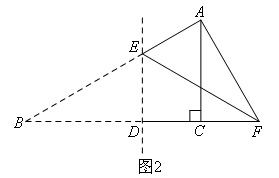

则∠FAC=90°-∠BAC=30°，
∴CF=2，
∴BD=DF=4．
综上，当△AEF为直角三角形时，BD的长为2或4．

略