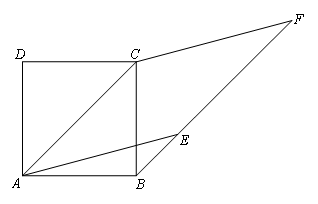
如图，四边形ABCD是正方形，过点B作BF∥AC，E是BF上一点，且四边形AEFC是菱形．则∠ACF是∠F的(    )倍．

思考方向：AC∥BF，可将正方形中的线段关系转移到菱形中．
如图，连接BD，交AC于点O，过点C作CG⊥BF于点G．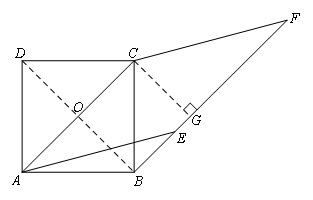

可证四边形BOCG是正方形，则OB=CG，
而在正方形ABCD中，，
由菱形AEFC，可证CG=CF．
在Rt△CFG中，可得∠F=30°，则∠ACF=150°，
故∠ACF=5∠F．
故选B．

略