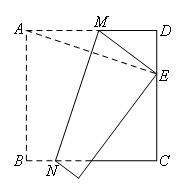
如图，将边长为12cm的正方形ABCD折叠，使得点A落在CD边上的点E处，折痕为MN．
若CE的长为8cm，则MN的长为( )
- A.12cm
- B.
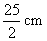
- C.
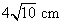
- D.
答案
正确答案：C
知识点：勾股定理 正方形的性质 翻折变换(折叠问题)
如图，设AE与MN的交点为G，过点N作NF⊥AD于点F．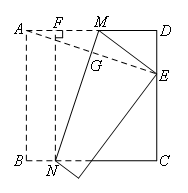
则∠NFM=∠D=90°，FN=AB=DA．
由折叠可知，∠AGM=90°，
∴∠DAE+∠AMG=90°．
∵∠FNM+∠AMG=90°，
∴∠DAE=∠FNM，
∴△ADE≌△NFM，
∴MN=AE．
∵正方形的边长为12cm，CE=8cm，
∴DE=4cm．
在Rt△ADE中，由勾股定理得，
，
∴
．
略
WORD格式（
