如图1，在四边形ABCD中，AB=CD，E，F分别为BC，AD的中点，连接EF并延长，与BA，
CD的延长线分别交于点M，N．连接BD，取BD的中点H，连接HE，HF，可以证明∠BME=∠CNE．
（1）如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E，F分别为BC，AD的中点，连接EF，与CD，
AB分别交于点M，N．类比上面的做法，为了证明△OMN是等腰三角形，下列辅助线的作法合适的是(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=13000
①利用题干当中的信息（图形1中的辅助线描述），
理解是如何证明得到∠BME=∠CNE．
∵F，H，E分别是AD，BD，BC的中点，
∴HF，HE分别是△ABD，△BCD的中位线，
∴HF∥AB，，HE∥CD，，
∴∠BME=∠HFE，∠CNE=∠HEF．
∵AB=CD，
∴HF=HE，
∴∠HFE=∠HEF，
∴∠BME=∠CNE．
问题出发点是，有多个中点时，可以构造中位线来解决问题．
主要利用了两个中点和一组线段长相等．
②题干条件与（1）中的条件只在图形形状上发生了变化，
“两个中点和一组线段长相等”都没有发生变化，属于不变特征，
所以考虑照搬题干中的辅助线：取BD的中点H，连接HE，HF．
③照搬图1中的分析思路，验证上述辅助线能够证明△OMN是等腰三角形．
如图，

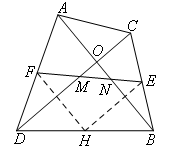
类比①中的分析可知，
HF∥AB，，HE∥CD，，
∴∠OMN=∠FEH，∠ONM =∠EFH．
∵AB=CD，
∴HF=HE，
∴∠FEH =∠EFH，
∴∠OMN =∠ONM，
即上述辅助线可以证明△OMN是等腰三角形．
故选B．

略