如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是( )
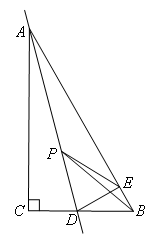
- A.
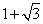
- B.
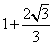
- C.
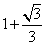
- D.
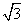
答案
正确答案:A
知识点:含30°角的直角三角形 轴对称路径最短问题
分析:△PEB的周长的最小,即PE+PB+BE的值最小,而BE是不变的,只需求PE+PB最小即可,B,E为两个定点,P为动点,AD为定直线,所求是PE+PB的最小值,从这些特征可以判断是轴对称路径最短问题.且C,E两点关于直线AD对称,即BD为PE+PB最小值。做题方法如下: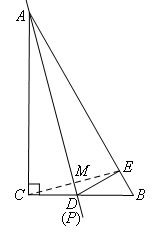
连接CE,交AD于M,
将△ABC沿直线AD翻折,点C和E重合.
∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD.
∴AD垂直平分CE,即C和E关于AD对称,CD=DE=1.
∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE.
∵∠DEA=90°,
∴∠DEB=90°.
∵∠B=60°,DE=1,![]()
∴![]()
故选A
略








