在正方形ABCD中,O是对角线BD的中点,点P是BD所在直线上的一个动点,PE⊥BC于E,PF⊥CD于F.如图1,当点P与点O重合时,猜测AP=EF且AP⊥EF,小明在证明AP=EF时想到了下列思路,你认为比较合理的是( )
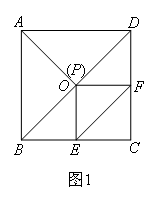
①延长FO交AB于点M,证明△AMO≌△FOE
②通过四边形PECF的面积与△AOD的面积相等来证明
③证明四边形PDFE是平行四边形,通过AO=OD=EF来证明
- A.①②③
- B.①②
- C.②③
- D.①③
答案
正确答案:A
知识点:类比探究
以上三种思路都可以走通,以思路①为例:
连接AC,则AC必过点O,延长FO交AB于M,由于O是BD中点,易证得△AOM≌△FEO,
则AO=EF,且∠AOM=∠FOC=∠OFE=45°,由此可证得AP⊥EF.
证明:
如图,连接AC,则AC必过点O,延长FO交AB于M;
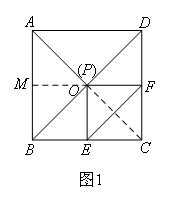
∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,
∴四边形OECF是正方形,
∴OM=OF=OE=AM,
∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,
∴△AMO≌△FOE,
∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,
故AP=EF,且AP⊥EF.
略








