(上接试题1)(2)设抛物线上一点P的横坐标为m,连接PB,PA,当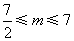 时,若存在△ABP,则△ABP面积的最大值为( )
时,若存在△ABP,则△ABP面积的最大值为( )
- A.
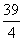
- B.9
- C.
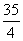
- D.7
答案
正确答案:C
1.解题要点
①分析目标△ABP,点A,B是定点,点P是动点,坐标系下表达斜放置的三角形面积,考虑利用分割求和中的铅垂法进行求解;
②由于点A(6,0),![]() ,点P可能落在直线AB的上方,也可能落在下方,所以需要进行分类,分别表达出每一段的面积,进而求面积最大值;
,点P可能落在直线AB的上方,也可能落在下方,所以需要进行分类,分别表达出每一段的面积,进而求面积最大值;
③在两定点一动点的铅垂法求面积时,过动点P作铅垂的线交直线AB于点E,将PE当底,发现△ABP的高是![]() ,表达面积即可.
,表达面积即可.
2.解题过程
∵![]()
∴![]() ,
,
由题意![]() ,
,
①当点P在直线AB上方的抛物线上时,即![]() 时,
时,
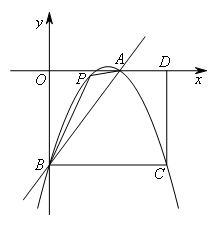
如图,过点P作PE∥y轴交直线AB于点E,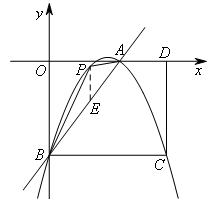
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 取最大值为
取最大值为![]() .
.
②当点P在直线AB下方的抛物线上时,即![]() 时,
时,
如图,过点P作PE∥y轴交直线AB于点E,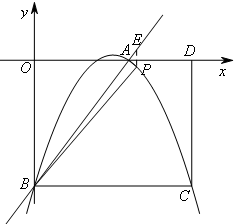
∴![]() ,
,
∴![]() ,
,
∴当m=7时,![]() 取最大值为7.
取最大值为7.
综上,△ABP面积的最大值为![]() .
.
略








